Microsoft Teamsの予期しないダウンロードエラーを修正する方法
Microsoft Teamsのダウンロードエラー「予期せぬエラー」でワークフローが滞っていませんか？専門家によるステップバイステップガイドと、クイックフィックスと高度なヒントで、すぐに問題を解決できます。再インストールは不要です！
球の表面積と体積を計算する公式
以下の記事で、Quantrimang.com を使って球の表面積と体積を計算する公式を学習し、復習しましょう。
目次
球体とは何ですか？
球は、r 3 次元空間内の特定の固定点 O から等距離にある点の軌跡です。点 O は球の中心と呼ばれ、その距離はr球の半径と呼ばれます。
球体とは何ですか？
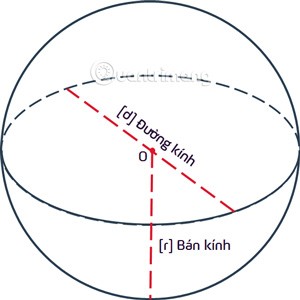
球は球の内部にある点の集合であり、球は球または中心が O で半径が r = OA の球と呼ばれます。
球の表面積と体積を計算する公式
球の表面積を計算する公式
球の表面積は大きな円の面積の 4 倍で、これは定数円周率の 4 倍に球の半径の 2 乗を掛けた値です。
球の体積を計算する公式:
球の体積は、円周率の 4 分の 3 に球の半径の 3 乗を掛けて計算されます。
そこには：
S球の表面積ですV球の体積ですr球の半径ですd球体です
球の半径を計算する式
ピラミッドに外接する球面には、底面に対して垂直な辺があります。
- Rd は底辺の半径です。
- hは底辺に垂直な辺の長さです。
たとえば、AB = 3a、BC = 4a、SA = 12a で、SA が底面に垂直である長方形の底面を持つピラミッド S.ABCD があるとします。角錐S.ABCDに外接する球の半径Rを計算します。
解決策: 私たちは
それで
正方四面体（これは式1の特殊なケースです）
正方形ブロック OABC は、OA、OB、OC が互いに垂直であり、次のようになります。
例えば：
四面体 OABC は、OA、OB、OC が互いに垂直で、外接球面の半径が です。四面体OABCの最大体積
解決策：私たちは
一方、次のようになります。
AM - GM 不等式によれば、次のようになります。
垂直柱の底面は内接多角形です。
そこには：
- Rdは底辺の半径です
- hは辺の長さです。
例 1:辺が a の立方体に外接する半径 R の球が与えられます。次の記述のうち正しいものはどれですか?
A.
B.
C.
D.
解決策: 私たちは
したがって答えは C です。
直角柱の頂点を頂点とする四面体の公式
四面体 (H1) の頂点は垂直柱 (H2) の頂点と同じなので、次のようになります。
底面に垂直な側面を持つピラミッドの球面の半径を計算する公式
ここで、R、dは底辺の半径です。 a、xはそれぞれ、側面と底面の交点の長さ、側面の上部から底面を見下ろした角度です。
または、次の式を使うこともできます
ここで、Rb は側面の外接半径、a は側面と底面の交点の長さです。
例えば：
正方形の底辺を持つ角錐 S.ABCD と、その底辺に垂直な平面に位置する、辺が√2a の正三角形 SAD が与えられます。角錐S.ABCDに外接する球の半径Rを計算します。
A.
B.
解決策: 私たちは
したがって正解はBです。
球の表面積と体積の計算例
レッスン 1 : 円周が 31.4 cm の円が与えられます。指定された円の半径に等しい半径を持つ球の体積を計算します。
賞：
円周 C = 2πr = 31.4 cm
=> 半径 r = C/2π = 5 cm
与えられた球の体積は次のようになります。
V = ⁴⁄₃πr³ = 4/3.3.14.(5)³ = 523.3 cm³
レッスン 2 : 直径 d = 4 cm の球の体積を計算します。
賞：
半径 r = d/2 = 2 cm
球の体積は次のとおりです。
V = ⁴⁄₃πr³ = 4/3.3.14.(2)³ = 33.49 cm³
レッスン3：
直径4aの円がその直径の周りを回転するとします。回転する固体の体積はいくらでしょうか?
解答: 直径 4a の円がその直径の周りを回転すると、直径 4a または半径 R = 2a の球が得られます。
球の体積は次のとおりです。
レッスン4：
半径R√3の球の面積は次のようになります。
A. 4√3πR2
B. 4πR2
C. 6πR2
D. 12πR2
解答: 式S = 4πR2を適用する。
半径R√3の球の表面積は、S = 4π(R√3)2 = 12πR2です。
したがって答えはDです。
2つの短い数式ですが、長期間覚えておくのは非常に困難です。記事をブックマークして、必要なときに開いてください。この記事がお役に立つことを願っております。
上記の球の表面積と体積を計算する公式に加えて、三角形、長方形、平行四辺形などの他の基本的な図形の面積を計算する公式も参照できます。 ..
Teams 会議でブレイクアウト ルームが表示されないのはなぜですか?
Teams 会議でブレイクアウトルームが表示されなくて困っていませんか？Teams でブレイクアウトルームが表示されない主な原因を解説します。ステップバイステップの解決方法に従って、数分でスムーズに機能するようにしましょう。主催者にも参加者にも最適です！
Microsoft Teams OneDriveのファイル同期エラーの解決
Microsoft Teams OneDriveのファイル同期エラーにうんざりしていませんか？ステップバイステップガイドに従って、Microsoft Teams OneDriveのファイル同期エラーを素早く解決しましょう。Teamsチャンネルでのスムーズな共同作業に役立つ実証済みの修正プログラムをご用意しています。今すぐエラーのないファイル同期を実現しましょう！
Microsoft Teams のハードエラーを修正する方法（2026 レジストリ修正）
Microsoft Teamsがハードエラーでクラッシュするのにうんざりしていませんか？ わずか数分で解決できる、実績のある2026レジストリ修正プログラムを入手しましょう。ステップバイステップガイド、スクリーンショット、そして永続的な問題解決のためのヒントをご紹介します。最新バージョンで動作します！
Microsoft Teamsチュートリアルヘルプエラーのトラブルシューティング
Microsoft Teamsチュートリアルヘルプのエラーでお困りですか？このよくある問題に対する、実証済みのステップバイステップの解決策をご覧ください。キャッシュをクリアし、Teamsを更新するなど、すぐにシームレスなコラボレーションを取り戻しましょう！
Microsoft Teams エラーのトラブルシューティング: 最初に確認すべきこと
Microsoft Teamsでエラーが発生していますか？このMicrosoft Teamsのトラブルシューティングガイドでは、エラーを迅速に解決するための最初のチェックポイントをステップバイステップでご紹介します。接続、キャッシュ、アップデートに関するクイックフィックスで、スムーズなチャットを再開できます。
Microsoft Teams アドインが Outlook に表示されないのはなぜですか?
Outlook に Microsoft Teams アドインが表示されなくて困っていませんか？主な原因と簡単なステップバイステップの修正方法をご紹介します。Teams と Outlook のシームレスな連携を簡単に復元できます。最新バージョンでご利用いただけます。
公共Wi-FiでのMicrosoft Teamsネットワークエラーの解決方法
公共Wi-FiでMicrosoft Teamsのネットワークエラーに悩まされていませんか？VPNの調整、ポートチェック、キャッシュクリアなどの即時修正で、通話や会議をスムーズに復旧できます。ステップバイステップガイドですぐに問題を解決できます。
Microsoft Teams のステータスが「離席中」のままになっているのはなぜですか?
Microsoft Teamsのステータスが「離席中」のままになって困っていませんか？アイドルタイムアウトや電源設定など、よくある原因と、すぐに「対応可能」に戻すためのステップバイステップの修正方法をご紹介します。最新のTeams機能にアップデートしました。
Microsoft Teams のようこそ画面の起動ループのトラブルシューティング
Microsoft Teamsのようこそ画面の起動ループに悩まされていませんか？Microsoft Teamsのようこそ画面の起動ループを解消するための実証済みのトラブルシューティング手順をお試しください。キャッシュのクリア、アプリのリセット、再インストールが可能です。数分でシームレスなコラボレーション環境を取り戻せます！
Microsoft Teamsはなぜ遅いのか？2026年にスピードアップするための10のヒント
Microsoft Teams の遅延にイライラしていませんか？Microsoft Teams が遅い理由を解明し、2026 年に劇的に高速化するための 10 の実証済みヒントを適用して、スムーズなコラボレーションを実現しましょう。
Microsoft Teams のショートカット エラーと起動時のクラッシュを解決する
Microsoft Teamsのショートカットエラーでワークフローが滞っていませんか？Microsoft Teamsのショートカットエラーや起動時のクラッシュを解決し、スムーズなコラボレーションを実現する実証済みの手順をご紹介します。素早く簡単に解決できる方法を解説しています。
直接リンク経由でMicrosoft Teamsの会議参加エラーを解決する
Microsoft Teamsの会議参加エラーでお困りですか？直接リンクから解決方法をご確認ください。シームレスに参加するためのクイックフィックス - 技術的なスキルは必要ありません！
Chromebook で Microsoft Teams のログインエラーを修正する方法
Chromebook で Microsoft Teams のログインエラーに困っていませんか？ログイン問題を素早く解決するためのステップバイステップの解決策をご紹介します。キャッシュのクリア、アプリのアップデートなど、スムーズなチームワークを実現しましょう。最新の Chrome OS で動作します！
Teamsカレンダーはどこにありますか？同期の問題のトラブルシューティング
Teamsのカレンダーがどこにあるのか分からず困っていませんか？Microsoft Teamsの同期に関する問題をステップバイステップで解決しましょう。専門家のヒントも満載で、カレンダービューを復元して簡単に同期できます。