ハードドライブへのアクセスを回復し、ハードドライブを開けないエラーを修正する方法
この記事では、ハードドライブが故障した場合に、アクセスを回復する方法をご紹介します。さあ、一緒に進めていきましょう！
正方形の対角線と長方形の対角線を計算する公式
正方形の対角線を計算する方法、長方形の対角線を計算する方法は、数学の問題や、設計や建設、手抜き、測定などの実用的なアプリケーションでよく使用されます... Quantrimang.com では、2 つの対角線の特性と計算式に関する知識をまとめていますので、学習、生活、仕事に応用する際に参照してください。
目次
正方形と長方形の対角線の長さは何ですか?
正方形または長方形の対角線は、向かい合う 2 つの角を結ぶ線です。すべての正方形と長方形には、等しい長さの 2 つの対角線があります。
正方形の対角線を計算する方法
正方形対角線の性質
- 正方形の 2 つの対角線は長さが等しく、垂直であり、それぞれの中心点で交差します。
- 内接円と外接円があり、両方の円の中心は一致し、正方形の 2 つの対角線の交点になります。
- 1 本の対角線で正方形が 2 つの直角二等辺三角形に分割されます。
- 角の二等分線、中線、垂直二等分線の交点はすべて 1 点に一致します。
- 長方形、平行四辺形、ひし形のすべての特性を持ちます。
正方形の対角線を計算する公式
正方形の性質によれば、正方形の 2 つの対角線は等しく、正方形の 1 つの対角線は正方形を 2 つの等しい面積の領域、つまり 2 つの直角二等辺三角形に分割します。したがって、正方形の対角線は、2 つの直角二等辺三角形の斜辺になります。
したがって、正方形の対角線を計算するには、ピタゴラスの定理を直角三角形に適用するだけです。
辺の長さが a の正方形 ABCD があるとします。対角線 AC は正方形を 2 つの直角三角形 ABC と ACD に分割します。
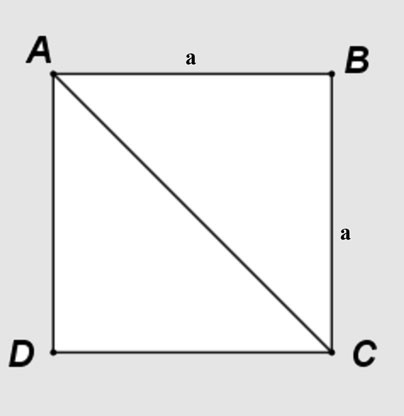
ピタゴラスの定理を直角二等辺三角形 ABC に適用すると、次のようになります。
⇒ ⇒
したがって、正方形の対角線の辺の長さは a です。
正方形の対角線を計算する例
例 1: 正方形の一辺は 3cm です。その正方形の対角線は、6cm、√18cm、5cm、それとも4cmでしょうか?
解決：
a) 正方形 ABC にピタゴラスの定理を適用すると、次のようになります。
AC² = AB² + BC² = 3² + 3² = 18
=> AC = cm
したがって、正方形の対角線は√18 cm です。
例2:
正方形の対角線の長さは 2dm です。その正方形の辺は、1cm、3/2cm、√2cm、それとも4/3cmでしょうか?
賞：
ピタゴラスの定理を直角三角形 ABC に適用しますが、この演習では対角線の長さ (AC = 2cm) が与えられ、辺 AB を計算します。
AC² = AB² + BC² = 2AB となります（AB = BC なので）
=> AB² = AC²/2 = 2²/2 = 2
=> AB = √2
長方形の対角線を計算する方法
長方形は 4 つの直角を持つ凸四辺形であり、2 つの対角線が等しい平行四辺形です。
長方形の対角線の性質
長方形の対角線には、長方形とその対角線に関する問題を解決するのに役立ついくつかの重要な特性があります。
- 長方形の対角線の長さは直角三角形の斜辺なので、2 辺の平方の合計の平方根に等しくなります。
- 対角線は長方形を等しい面積の 2 つの直角三角形に分割します。したがって、長方形の対角線は長方形の対称軸です。
- 長方形の 2 つの対角線は等しく、各線の中点で交差し、4 つの二等辺三角形を形成します。
長方形の対角線を計算する公式
上記の長方形の対角線の特性から、ピタゴラスの定理を使用して長方形の対角線の長さを計算できます。
以下に示すように、長さ a、幅 b、対角線 AC の長方形 ABCD があるとします。
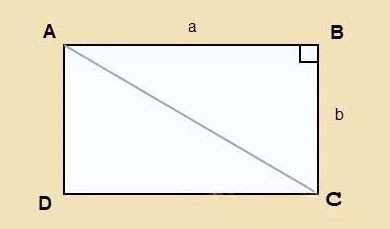
ピタゴラスの定理を直角三角形 ABC に適用します。
⇒ ⇒
したがって、長さ a 、幅 b の長方形の対角線は次のようになります。
したがって、長方形の対角線の長さは、長方形の 2 辺 (長さと幅) の平方の合計の平方根に等しくなります。
したがって、ピタゴラスの定理を適用するだけで、正方形または長方形の対角線を計算できます。
長方形の対角線の計算例
長さが 10dm、幅が 5dm の長方形の対角線の長さを計算します。
解決：
長方形の対角線の長さをa（a > 0, dm）とする。
ピタゴラスの定理を適用すると、長方形の対角線の長さは次のようになります。
a2 = 102 + 52 = 125
=> a = 5√5 dm
四辺形が長方形であることを証明する例。
長方形の対角線を計算する特性と公式は、四辺形が長方形であることを証明するいくつかの問題を解決するために適用できます。
四角形 ABCD には互いに直交する 2 つの対角線があります。 E、F、G、H をそれぞれ辺 AB、BC、CD、AD の中点とします。四辺形 EFGH はどのような形ですか?なぜ？
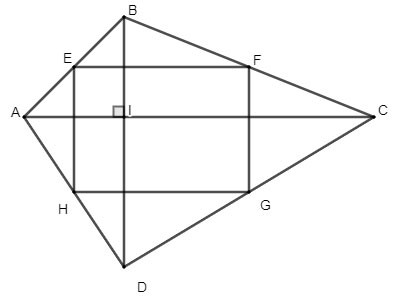
解決：
EはABの中点なので、HはADの中点です。
=> EHは三角形ABDの中線です。
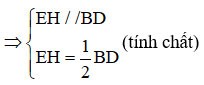（1）
FはBCの中点なので、GはCDの中点である。
=> FGは三角形BCDの中線です
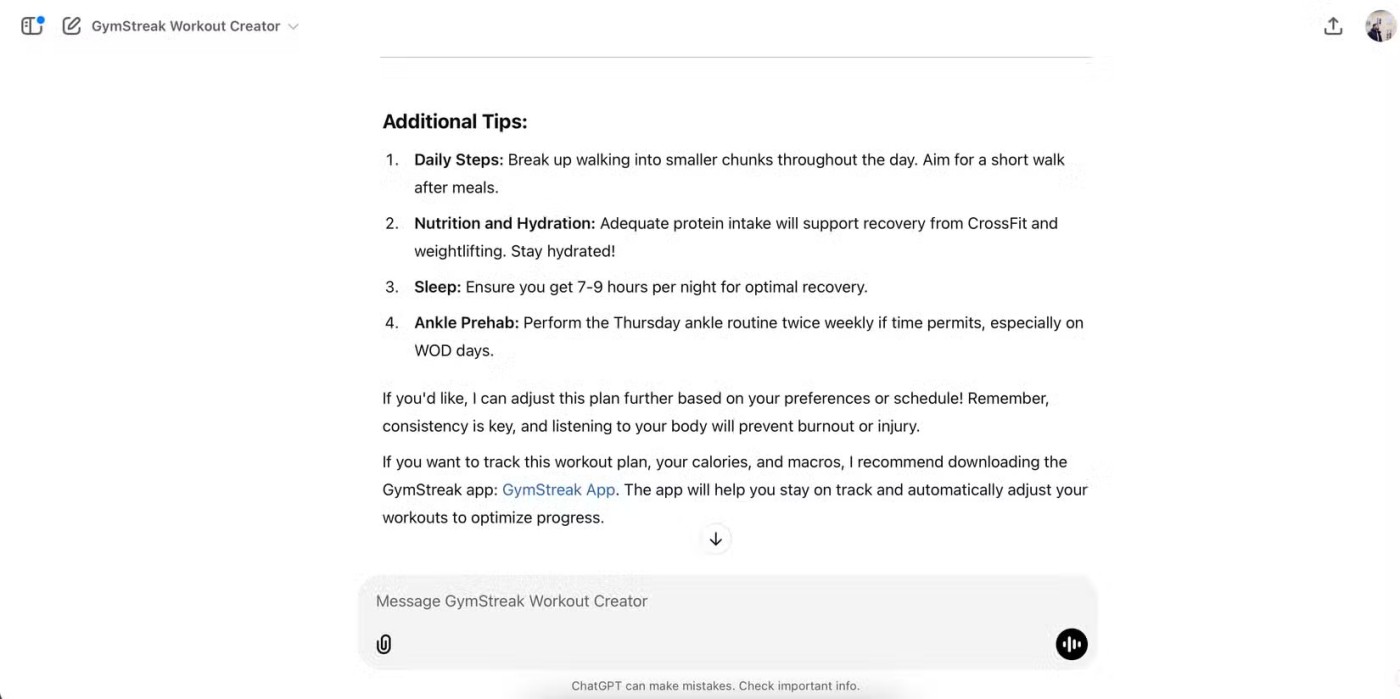（2）
(1)と(2)から =>
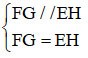
四辺形 EFGH を考えます。
FG // EH
FG = EH
=> EFGHは平行四辺形です（認識記号）
一方で：
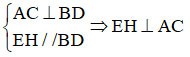
以下も含まれています:
E は AB の中点、F は BC の中点です。
=> EFは三角形ABCの中線です
=> EF // AC
しかし、EH⊥AC => EH⊥EF
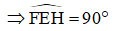
平行四辺形EFGHは直角である
=> EFGHは長方形です
AirPodsで会話認識とライブリスニングを使用する方法
一見すると、AirPodsは他の完全ワイヤレスイヤホンと何ら変わりません。しかし、あまり知られていないいくつかの機能が発見されたことで、すべてが変わりました。
IOS 26のすべて
Apple は、まったく新しいすりガラスデザイン、よりスマートなエクスペリエンス、おなじみのアプリの改善を伴うメジャーアップデートである iOS 26 を発表しました。
2025年の学生に最適なノートパソコン
学生は学習のために特定のタイプのノートパソコンを必要とします。専攻分野で十分なパフォーマンスを発揮できるだけでなく、一日中持ち運べるほどコンパクトで軽量であることも重要です。
Windows 10にプリンターを追加する方法
Windows 10 にプリンターを追加するのは簡単ですが、有線デバイスの場合のプロセスはワイヤレス デバイスの場合とは異なります。
最高の精度でコンピューターのRAMをチェックし、RAMエラーをチェックする方法
ご存知の通り、RAMはコンピューターにとって非常に重要なハードウェア部品であり、データ処理のためのメモリとして機能し、ノートパソコンやPCの速度を決定づける要因です。以下の記事では、WebTech360がWindowsでソフトウェアを使ってRAMエラーをチェックする方法をいくつかご紹介します。
通常のテレビとスマートテレビの違い
スマートテレビはまさに世界を席巻しています。数多くの優れた機能とインターネット接続により、テクノロジーはテレビの視聴方法を変えました。
なぜ冷凍庫にはライトがないのに、冷蔵庫にはライトがあるのでしょうか?
冷蔵庫は家庭ではよく使われる家電製品です。冷蔵庫には通常 2 つの部屋があり、冷蔵室は広く、ユーザーが開けるたびに自動的に点灯するライトが付いていますが、冷凍室は狭く、ライトはありません。
Wi-Fiの速度低下を引き起こすネットワーク混雑を解決する2つの方法
Wi-Fi ネットワークは、ルーター、帯域幅、干渉以外にも多くの要因の影響を受けますが、ネットワークを強化する賢い方法がいくつかあります。
Tenorshare Reibootを使ってデータ損失なくiOS 17からiOS 16にダウングレードする方法
お使いの携帯電話で安定した iOS 16 に戻したい場合は、iOS 17 をアンインストールして iOS 17 から 16 にダウングレードするための基本ガイドを以下に示します。
ヨーグルトを毎日食べると体に何が起こるのでしょうか？
ヨーグルトは素晴らしい食べ物です。ヨーグルトを毎日食べるのは良いことでしょうか？ヨーグルトを毎日食べると、身体はどう変わるのでしょうか？一緒に調べてみましょう！
健康に最も良いお米の種類は何ですか？
この記事では、最も栄養価の高い米の種類と、どの米を選んだとしてもその健康効果を最大限に引き出す方法について説明します。
朝時間通りに起きる方法
睡眠スケジュールと就寝時の習慣を確立し、目覚まし時計を変え、食生活を調整することは、よりよく眠り、朝時間通りに起きるのに役立つ対策の一部です。
Rent Please! をプレイするためのヒント初心者向け大家シミュレーション
レンタルして下さい！ Landlord Sim は、iOS および Android 向けのシミュレーション モバイル ゲームです。あなたはアパートの大家としてプレイし、アパートの内装をアップグレードして入居者を受け入れる準備をしながら、アパートの賃貸を始めます。
最新のバスルームタワーディフェンスコードとコードの入力方法
Bathroom Tower Defense Roblox ゲーム コードを入手して、魅力的な報酬と引き換えましょう。これらは、より高いダメージを与えるタワーをアップグレードしたり、ロックを解除したりするのに役立ちます。